The functions in this section perform various geometrical transformations of 2D images. They do not change the image content but deform the pixel grid and map this deformed grid to the destination image. In fact, to avoid sampling artifacts, the mapping is done in the reverse order, from destination to the source. That is, for each pixel 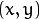 of the destination image, the functions compute coordinates of the corresponding “donor” pixel in the source image and copy the pixel value:
of the destination image, the functions compute coordinates of the corresponding “donor” pixel in the source image and copy the pixel value:
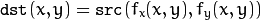
In case when you specify the forward mapping
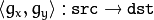 , the OpenCV functions first compute the corresponding inverse mapping
, the OpenCV functions first compute the corresponding inverse mapping
 and then use the above formula.
and then use the above formula.
The actual implementations of the geometrical transformations, from the most generic remap() and to the simplest and the fastest resize() , need to solve two main problems with the above formula:
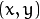 , either one of
, either one of
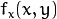 , or
, or
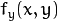 , or both of them may fall outside of the image. In this case, an extrapolation method needs to be used. OpenCV provides the same selection of extrapolation methods as in the filtering functions. In addition, it provides the method BORDER_TRANSPARENT . This means that the corresponding pixels in the destination image will not be modified at all.
, or both of them may fall outside of the image. In this case, an extrapolation method needs to be used. OpenCV provides the same selection of extrapolation methods as in the filtering functions. In addition, it provides the method BORDER_TRANSPARENT . This means that the corresponding pixels in the destination image will not be modified at all.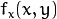 and
and
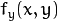 are floating-point numbers. This means that
are floating-point numbers. This means that
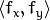 can be either an affine or perspective transformation, or radial lens distortion correction, and so on. So, a pixel value at fractional coordinates needs to be retrieved. In the simplest case, the coordinates can be just rounded to the nearest integer coordinates and the corresponding pixel can be used. This is called a nearest-neighbor interpolation. However, a better result can be achieved by using more sophisticated interpolation methods
, where a polynomial function is fit into some neighborhood of the computed pixel
can be either an affine or perspective transformation, or radial lens distortion correction, and so on. So, a pixel value at fractional coordinates needs to be retrieved. In the simplest case, the coordinates can be just rounded to the nearest integer coordinates and the corresponding pixel can be used. This is called a nearest-neighbor interpolation. However, a better result can be achieved by using more sophisticated interpolation methods
, where a polynomial function is fit into some neighborhood of the computed pixel
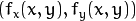 , and then the value of the polynomial at
, and then the value of the polynomial at
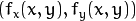 is taken as the interpolated pixel value. In OpenCV, you can choose between several interpolation methods. See
resize() for details.
is taken as the interpolated pixel value. In OpenCV, you can choose between several interpolation methods. See
resize() for details.Converts image transformation maps from one representation to another.
| Parameters: |
|
|---|
The function converts a pair of maps for
remap() from one representation to another. The following options ( (map1.type(), map2.type()) 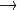 (dstmap1.type(), dstmap2.type()) ) are supported:
(dstmap1.type(), dstmap2.type()) ) are supported:
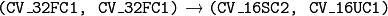 . This is the most frequently used conversion operation, in which the original floating-point maps (see
remap() ) are converted to a more compact and much faster fixed-point representation. The first output array contains the rounded coordinates and the second array (created only when nninterpolation=false ) contains indices in the interpolation tables.
. This is the most frequently used conversion operation, in which the original floating-point maps (see
remap() ) are converted to a more compact and much faster fixed-point representation. The first output array contains the rounded coordinates and the second array (created only when nninterpolation=false ) contains indices in the interpolation tables.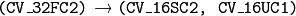 . The same as above but the original maps are stored in one 2-channel matrix.
. The same as above but the original maps are stored in one 2-channel matrix.See also
Calculates an affine transform from three pairs of the corresponding points.
| Parameters: |
|
|---|
The function calculates the 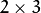 matrix of an affine transform so that:
matrix of an affine transform so that:

where
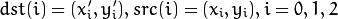
See also
Calculates a perspective transform from four pairs of the corresponding points.
| Parameters: |
|
|---|
The function calculates the 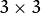 matrix of a perspective transform so that:
matrix of a perspective transform so that:

where
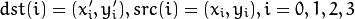
Retrieves a pixel rectangle from an image with sub-pixel accuracy.
| Parameters: |
|
|---|
The function getRectSubPix extracts pixels from src :
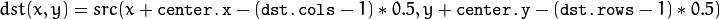
where the values of the pixels at non-integer coordinates are retrieved using bilinear interpolation. Every channel of multi-channel images is processed independently. While the center of the rectangle must be inside the image, parts of the rectangle may be outside. In this case, the replication border mode (see borderInterpolate() ) is used to extrapolate the pixel values outside of the image.
See also
Calculates an affine matrix of 2D rotation.
| Parameters: |
|
|---|
The function calculates the following matrix:
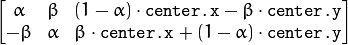
where
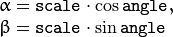
The transformation maps the rotation center to itself. If this is not the target, adjust the shift.
See also
Inverts an affine transformation.
| Parameters: |
|
|---|
The function computes an inverse affine transformation represented by
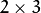 matrix M :
matrix M :
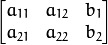
The result is also a
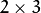 matrix of the same type as M .
matrix of the same type as M .
Remaps an image to polar space.
| Parameters: |
|
|---|
The function cvLinearPolar transforms the source image using the following transformation:
Forward transformation (CV_WARP_INVERSE_MAP is not set):
Inverse transformation (CV_WARP_INVERSE_MAP is set):
where
The function can not operate in-place.
Note
Remaps an image to log-polar space.
| Parameters: |
|
|---|
The function cvLogPolar transforms the source image using the following transformation:
Forward transformation (CV_WARP_INVERSE_MAP is not set):
Inverse transformation (CV_WARP_INVERSE_MAP is set):
where
The function emulates the human “foveal” vision and can be used for fast scale and rotation-invariant template matching, for object tracking and so forth. The function can not operate in-place.
Note
Applies a generic geometrical transformation to an image.
| Parameters: |
|
|---|
The function remap transforms the source image using the specified map:
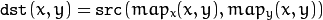
where values of pixels with non-integer coordinates are computed using one of available interpolation methods.
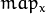 and
and
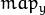 can be encoded as separate floating-point maps in
can be encoded as separate floating-point maps in
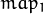 and
and
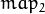 respectively, or interleaved floating-point maps of
respectively, or interleaved floating-point maps of
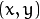 in
in
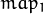 , or
fixed-point maps created by using
convertMaps() . The reason you might want to convert from floating to fixed-point
representations of a map is that they can yield much faster (~2x) remapping operations. In the converted case,
, or
fixed-point maps created by using
convertMaps() . The reason you might want to convert from floating to fixed-point
representations of a map is that they can yield much faster (~2x) remapping operations. In the converted case,
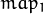 contains pairs (cvFloor(x), cvFloor(y)) and
contains pairs (cvFloor(x), cvFloor(y)) and
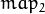 contains indices in a table of interpolation coefficients.
contains indices in a table of interpolation coefficients.
This function cannot operate in-place.
Resizes an image.
| Parameters: |
|
|---|
The function resize resizes the image src down to or up to the specified size. Note that the initial dst type or size are not taken into account. Instead, the size and type are derived from the src,``dsize``,``fx`` , and fy . If you want to resize src so that it fits the pre-created dst , you may call the function as follows:
// explicitly specify dsize=dst.size(); fx and fy will be computed from that.
resize(src, dst, dst.size(), 0, 0, interpolation);
If you want to decimate the image by factor of 2 in each direction, you can call the function this way:
// specify fx and fy and let the function compute the destination image size.
resize(src, dst, Size(), 0.5, 0.5, interpolation);
To shrink an image, it will generally look best with CV_INTER_AREA interpolation, whereas to enlarge an image, it will generally look best with CV_INTER_CUBIC (slow) or CV_INTER_LINEAR (faster but still looks OK).
See also
Applies an affine transformation to an image.
| Parameters: |
|
|---|
The function warpAffine transforms the source image using the specified matrix:
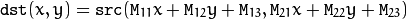
when the flag WARP_INVERSE_MAP is set. Otherwise, the transformation is first inverted with invertAffineTransform() and then put in the formula above instead of M . The function cannot operate in-place.
See also
warpPerspective(), resize(), remap(), getRectSubPix(), transform()
Note
cvGetQuadrangleSubPix is similar to cvWarpAffine, but the outliers are extrapolated using replication border mode.
Applies a perspective transformation to an image.
| Parameters: |
|
|---|
The function warpPerspective transforms the source image using the specified matrix:
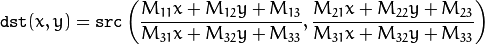
when the flag WARP_INVERSE_MAP is set. Otherwise, the transformation is first inverted with invert() and then put in the formula above instead of M . The function cannot operate in-place.
See also
warpAffine(), resize(), remap(), getRectSubPix(), perspectiveTransform()
Computes the undistortion and rectification transformation map.
| Parameters: |
|
|---|
The function computes the joint undistortion and rectification transformation and represents the result in the form of maps for remap() . The undistorted image looks like original, as if it is captured with a camera using the camera matrix =newCameraMatrix and zero distortion. In case of a monocular camera, newCameraMatrix is usually equal to cameraMatrix , or it can be computed by getOptimalNewCameraMatrix() for a better control over scaling. In case of a stereo camera, newCameraMatrix is normally set to P1 or P2 computed by stereoRectify() .
Also, this new camera is oriented differently in the coordinate space, according to R . That, for example, helps to align two heads of a stereo camera so that the epipolar lines on both images become horizontal and have the same y- coordinate (in case of a horizontally aligned stereo camera).
The function actually builds the maps for the inverse mapping algorithm that is used by
remap() . That is, for each pixel
 in the destination (corrected and rectified) image, the function computes the corresponding coordinates in the source image (that is, in the original image from camera). The following process is applied:
in the destination (corrected and rectified) image, the function computes the corresponding coordinates in the source image (that is, in the original image from camera). The following process is applied:
![\begin{array}{l} x \leftarrow (u - {c'}_x)/{f'}_x \\ y \leftarrow (v - {c'}_y)/{f'}_y \\{[X\,Y\,W]} ^T \leftarrow R^{-1}*[x \, y \, 1]^T \\ x' \leftarrow X/W \\ y' \leftarrow Y/W \\ x" \leftarrow x' (1 + k_1 r^2 + k_2 r^4 + k_3 r^6) + 2p_1 x' y' + p_2(r^2 + 2 x'^2) \\ y" \leftarrow y' (1 + k_1 r^2 + k_2 r^4 + k_3 r^6) + p_1 (r^2 + 2 y'^2) + 2 p_2 x' y' \\ map_x(u,v) \leftarrow x" f_x + c_x \\ map_y(u,v) \leftarrow y" f_y + c_y \end{array}](../../../_images/math/8808430360ef87d99c3a5725cd2ba7d2852ba689.png)
where
![(k_1, k_2, p_1, p_2[, k_3])](../../../_images/math/1cf983c88f452726ea3655ebe8d92882db4eff90.png) are the distortion coefficients.
are the distortion coefficients.
In case of a stereo camera, this function is called twice: once for each camera head, after stereoRectify() , which in its turn is called after stereoCalibrate() . But if the stereo camera was not calibrated, it is still possible to compute the rectification transformations directly from the fundamental matrix using stereoRectifyUncalibrated() . For each camera, the function computes homography H as the rectification transformation in a pixel domain, not a rotation matrix R in 3D space. R can be computed from H as
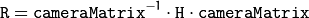
where cameraMatrix can be chosen arbitrarily.
Returns the default new camera matrix.
| Parameters: |
|
|---|
The function returns the camera matrix that is either an exact copy of the input cameraMatrix (when centerPrinicipalPoint=false ), or the modified one (when centerPrincipalPoint=true).
In the latter case, the new camera matrix will be:

where
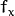 and
and
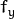 are
are
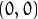 and
and
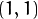 elements of cameraMatrix , respectively.
elements of cameraMatrix , respectively.
By default, the undistortion functions in OpenCV (see initUndistortRectifyMap(), undistort()) do not move the principal point. However, when you work with stereo, it is important to move the principal points in both views to the same y-coordinate (which is required by most of stereo correspondence algorithms), and may be to the same x-coordinate too. So, you can form the new camera matrix for each view where the principal points are located at the center.
Transforms an image to compensate for lens distortion.
| Parameters: |
|
|---|
The function transforms an image to compensate radial and tangential lens distortion.
The function is simply a combination of initUndistortRectifyMap() (with unity R ) and remap() (with bilinear interpolation). See the former function for details of the transformation being performed.
Those pixels in the destination image, for which there is no correspondent pixels in the source image, are filled with zeros (black color).
A particular subset of the source image that will be visible in the corrected image can be regulated by newCameraMatrix . You can use getOptimalNewCameraMatrix() to compute the appropriate newCameraMatrix depending on your requirements.
The camera matrix and the distortion parameters can be determined using
calibrateCamera() . If the resolution of images is different from the resolution used at the calibration stage,
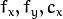 and
and
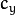 need to be scaled accordingly, while the distortion coefficients remain the same.
need to be scaled accordingly, while the distortion coefficients remain the same.
Computes the ideal point coordinates from the observed point coordinates.
| Parameters: |
|
|---|
The function is similar to undistort() and initUndistortRectifyMap() but it operates on a sparse set of points instead of a raster image. Also the function performs a reverse transformation to projectPoints() . In case of a 3D object, it does not reconstruct its 3D coordinates, but for a planar object, it does, up to a translation vector, if the proper R is specified.
// (u,v) is the input point, (u', v') is the output point
// camera_matrix=[fx 0 cx; 0 fy cy; 0 0 1]
// P=[fx' 0 cx' tx; 0 fy' cy' ty; 0 0 1 tz]
x" = (u - cx)/fx
y" = (v - cy)/fy
(x',y') = undistort(x",y",dist_coeffs)
[X,Y,W]T = R*[x' y' 1]T
x = X/W, y = Y/W
// only performed if P=[fx' 0 cx' [tx]; 0 fy' cy' [ty]; 0 0 1 [tz]] is specified
u' = x*fx' + cx'
v' = y*fy' + cy',
where undistort() is an approximate iterative algorithm that estimates the normalized original point coordinates out of the normalized distorted point coordinates (“normalized” means that the coordinates do not depend on the camera matrix).
The function can be used for both a stereo camera head or a monocular camera (when R is empty).