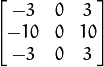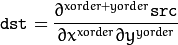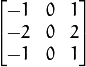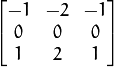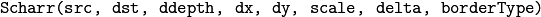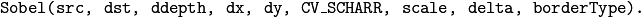Image Filtering
Functions and classes described in this section are used to perform various linear or non-linear filtering operations on 2D images (represented as
Mat()‘s). It means that for each pixel location
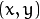 in the source image (normally, rectangular), its neighborhood is considered and used to compute the response. In case of a linear filter, it is a weighted sum of pixel values. In case of morphological operations, it is the minimum or maximum values, and so on. The computed response is stored in the destination image at the same location
in the source image (normally, rectangular), its neighborhood is considered and used to compute the response. In case of a linear filter, it is a weighted sum of pixel values. In case of morphological operations, it is the minimum or maximum values, and so on. The computed response is stored in the destination image at the same location
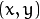 . It means that the output image will be of the same size as the input image. Normally, the functions support multi-channel arrays, in which case every channel is processed independently. Therefore, the output image will also have the same number of channels as the input one.
. It means that the output image will be of the same size as the input image. Normally, the functions support multi-channel arrays, in which case every channel is processed independently. Therefore, the output image will also have the same number of channels as the input one.
Another common feature of the functions and classes described in this section is that, unlike simple arithmetic functions, they need to extrapolate values of some non-existing pixels. For example, if you want to smooth an image using a Gaussian
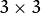 filter, then, when processing the left-most pixels in each row, you need pixels to the left of them, that is, outside of the image. You can let these pixels be the same as the left-most image pixels (“replicated border” extrapolation method), or assume that all the non-existing pixels are zeros (“constant border” extrapolation method), and so on.
OpenCV enables you to specify the extrapolation method. For details, see the function borderInterpolate and discussion of the borderType parameter in the section and various functions below.
filter, then, when processing the left-most pixels in each row, you need pixels to the left of them, that is, outside of the image. You can let these pixels be the same as the left-most image pixels (“replicated border” extrapolation method), or assume that all the non-existing pixels are zeros (“constant border” extrapolation method), and so on.
OpenCV enables you to specify the extrapolation method. For details, see the function borderInterpolate and discussion of the borderType parameter in the section and various functions below.
/*
Various border types, image boundaries are denoted with '|'
* BORDER_REPLICATE: aaaaaa|abcdefgh|hhhhhhh
* BORDER_REFLECT: fedcba|abcdefgh|hgfedcb
* BORDER_REFLECT_101: gfedcb|abcdefgh|gfedcba
* BORDER_WRAP: cdefgh|abcdefgh|abcdefg
* BORDER_CONSTANT: iiiiii|abcdefgh|iiiiiii with some specified 'i'
*/
Note
- (Python) A complete example illustrating different morphological operations like erode/dilate, open/close, blackhat/tophat ... can be found at opencv_source_code/samples/python2/morphology.py
bilateralFilter
Applies the bilateral filter to an image.
-
C++: void bilateralFilter(InputArray src, OutputArray dst, int d, double sigmaColor, double sigmaSpace, int borderType=BORDER_DEFAULT )
-
Python: cv2.bilateralFilter(src, d, sigmaColor, sigmaSpace[, dst[, borderType]]) → dst
| Parameters: |
- src – Source 8-bit or floating-point, 1-channel or 3-channel image.
- dst – Destination image of the same size and type as src .
- d – Diameter of each pixel neighborhood that is used during filtering. If it is non-positive, it is computed from sigmaSpace .
- sigmaColor – Filter sigma in the color space. A larger value of the parameter means that farther colors within the pixel neighborhood (see sigmaSpace ) will be mixed together, resulting in larger areas of semi-equal color.
- sigmaSpace – Filter sigma in the coordinate space. A larger value of the parameter means that farther pixels will influence each other as long as their colors are close enough (see sigmaColor ). When d>0 , it specifies the neighborhood size regardless of sigmaSpace . Otherwise, d is proportional to sigmaSpace .
|
|---|
The function applies bilateral filtering to the input image, as described in
http://www.dai.ed.ac.uk/CVonline/LOCAL_COPIES/MANDUCHI1/Bilateral_Filtering.html
bilateralFilter can reduce unwanted noise very well while keeping edges fairly sharp. However, it is very slow compared to most filters.
Sigma values: For simplicity, you can set the 2 sigma values to be the same. If they are small (< 10), the filter will not have much effect, whereas if they are large (> 150), they will have a very strong effect, making the image look “cartoonish”.
Filter size: Large filters (d > 5) are very slow, so it is recommended to use d=5 for real-time applications, and perhaps d=9 for offline applications that need heavy noise filtering.
This filter does not work inplace.
blur
Blurs an image using the normalized box filter.
-
C++: void blur(InputArray src, OutputArray dst, Size ksize, Point anchor=Point(-1,-1), int borderType=BORDER_DEFAULT )
-
Python: cv2.blur(src, ksize[, dst[, anchor[, borderType]]]) → dst
| Parameters: |
- src – input image; it can have any number of channels, which are processed independently, but the depth should be CV_8U, CV_16U, CV_16S, CV_32F or CV_64F.
- dst – output image of the same size and type as src.
- ksize – blurring kernel size.
- anchor – anchor point; default value Point(-1,-1) means that the anchor is at the kernel center.
- borderType – border mode used to extrapolate pixels outside of the image.
|
|---|
The function smoothes an image using the kernel:
The call blur(src, dst, ksize, anchor, borderType) is equivalent to boxFilter(src, dst, src.type(), anchor, true, borderType) .
boxFilter
Blurs an image using the box filter.
-
C++: void boxFilter(InputArray src, OutputArray dst, int ddepth, Size ksize, Point anchor=Point(-1,-1), bool normalize=true, int borderType=BORDER_DEFAULT )
-
Python: cv2.boxFilter(src, ddepth, ksize[, dst[, anchor[, normalize[, borderType]]]]) → dst
| Parameters: |
- src – input image.
- dst – output image of the same size and type as src.
- ddepth – the output image depth (-1 to use src.depth()).
- ksize – blurring kernel size.
- anchor – anchor point; default value Point(-1,-1) means that the anchor is at the kernel center.
- normalize – flag, specifying whether the kernel is normalized by its area or not.
- borderType – border mode used to extrapolate pixels outside of the image.
|
|---|
The function smoothes an image using the kernel:
where
Unnormalized box filter is useful for computing various integral characteristics over each pixel neighborhood, such as covariance matrices of image derivatives (used in dense optical flow algorithms, and so on). If you need to compute pixel sums over variable-size windows, use integral() .
buildPyramid
Constructs the Gaussian pyramid for an image.
-
C++: void buildPyramid(InputArray src, OutputArrayOfArrays dst, int maxlevel, int borderType=BORDER_DEFAULT )
| Parameters: |
- src – Source image. Check pyrDown() for the list of supported types.
- dst – Destination vector of maxlevel+1 images of the same type as src . dst[0] will be the same as src . dst[1] is the next pyramid layer, a smoothed and down-sized src , and so on.
- maxlevel – 0-based index of the last (the smallest) pyramid layer. It must be non-negative.
- borderType – Pixel extrapolation method (BORDER_CONSTANT don’t supported). See borderInterpolate for details.
|
|---|
The function constructs a vector of images and builds the Gaussian pyramid by recursively applying
pyrDown() to the previously built pyramid layers, starting from dst[0]==src .
dilate
Dilates an image by using a specific structuring element.
-
C++: void dilate(InputArray src, OutputArray dst, InputArray kernel, Point anchor=Point(-1,-1), int iterations=1, int borderType=BORDER_CONSTANT, const Scalar& borderValue=morphologyDefaultBorderValue() )
-
Python: cv2.dilate(src, kernel[, dst[, anchor[, iterations[, borderType[, borderValue]]]]]) → dst
-
C: void cvDilate(const CvArr* src, CvArr* dst, IplConvKernel* element=NULL, int iterations=1 )
| Parameters: |
- src – input image; the number of channels can be arbitrary, but the depth should be one of CV_8U, CV_16U, CV_16S, CV_32F` or ``CV_64F.
- dst – output image of the same size and type as src.
- kernel – structuring element used for dilation; if elemenat=Mat() , a 3 x 3 rectangular structuring element is used. Kernel can be created using getStructuringElement()
- anchor – position of the anchor within the element; default value (-1, -1) means that the anchor is at the element center.
- iterations – number of times dilation is applied.
- borderType – pixel extrapolation method (see borderInterpolate for details).
- borderValue – border value in case of a constant border
|
|---|
The function dilates the source image using the specified structuring element that determines the shape of a pixel neighborhood over which the maximum is taken:
The function supports the in-place mode. Dilation can be applied several ( iterations ) times. In case of multi-channel images, each channel is processed independently.
Note
- An example using the morphological dilate operation can be found at opencv_source_code/samples/cpp/morphology2.cpp
erode
Erodes an image by using a specific structuring element.
-
C++: void erode(InputArray src, OutputArray dst, InputArray kernel, Point anchor=Point(-1,-1), int iterations=1, int borderType=BORDER_CONSTANT, const Scalar& borderValue=morphologyDefaultBorderValue() )
-
Python: cv2.erode(src, kernel[, dst[, anchor[, iterations[, borderType[, borderValue]]]]]) → dst
-
C: void cvErode(const CvArr* src, CvArr* dst, IplConvKernel* element=NULL, int iterations=1)
| Parameters: |
- src – input image; the number of channels can be arbitrary, but the depth should be one of CV_8U, CV_16U, CV_16S, CV_32F` or ``CV_64F.
- dst – output image of the same size and type as src.
- kernel – structuring element used for erosion; if element=Mat() , a 3 x 3 rectangular structuring element is used. Kernel can be created using getStructuringElement().
- anchor – position of the anchor within the element; default value (-1, -1) means that the anchor is at the element center.
- iterations – number of times erosion is applied.
- borderType – pixel extrapolation method (see borderInterpolate for details).
- borderValue – border value in case of a constant border
|
|---|
The function erodes the source image using the specified structuring element that determines the shape of a pixel neighborhood over which the minimum is taken:
The function supports the in-place mode. Erosion can be applied several ( iterations ) times. In case of multi-channel images, each channel is processed independently.
Note
- An example using the morphological erode operation can be found at opencv_source_code/samples/cpp/morphology2.cpp
filter2D
Convolves an image with the kernel.
-
C++: void filter2D(InputArray src, OutputArray dst, int ddepth, InputArray kernel, Point anchor=Point(-1,-1), double delta=0, int borderType=BORDER_DEFAULT )
-
Python: cv2.filter2D(src, ddepth, kernel[, dst[, anchor[, delta[, borderType]]]]) → dst
-
C: void cvFilter2D(const CvArr* src, CvArr* dst, const CvMat* kernel, CvPoint anchor=cvPoint(-1,-1) )
-
The function applies an arbitrary linear filter to an image. In-place operation is supported. When the aperture is partially outside the image, the function interpolates outlier pixel values according to the specified border mode.
The function does actually compute correlation, not the convolution:
That is, the kernel is not mirrored around the anchor point. If you need a real convolution, flip the kernel using
flip() and set the new anchor to (kernel.cols - anchor.x - 1, kernel.rows - anchor.y - 1) .
The function uses the DFT-based algorithm in case of sufficiently large kernels (~``11 x 11`` or larger) and the direct algorithm for small kernels.
GaussianBlur
Blurs an image using a Gaussian filter.
-
C++: void GaussianBlur(InputArray src, OutputArray dst, Size ksize, double sigmaX, double sigmaY=0, int borderType=BORDER_DEFAULT )
-
Python: cv2.GaussianBlur(src, ksize, sigmaX[, dst[, sigmaY[, borderType]]]) → dst
| Parameters: |
- src – input image; the image can have any number of channels, which are processed independently, but the depth should be CV_8U, CV_16U, CV_16S, CV_32F or CV_64F.
- dst – output image of the same size and type as src.
- ksize – Gaussian kernel size. ksize.width and ksize.height can differ but they both must be positive and odd. Or, they can be zero’s and then they are computed from sigma* .
- sigmaX – Gaussian kernel standard deviation in X direction.
- sigmaY – Gaussian kernel standard deviation in Y direction; if sigmaY is zero, it is set to be equal to sigmaX, if both sigmas are zeros, they are computed from ksize.width and ksize.height , respectively (see getGaussianKernel() for details); to fully control the result regardless of possible future modifications of all this semantics, it is recommended to specify all of ksize, sigmaX, and sigmaY.
- borderType – pixel extrapolation method (see borderInterpolate for details).
|
|---|
The function convolves the source image with the specified Gaussian kernel. In-place filtering is supported.
getDerivKernels
Returns filter coefficients for computing spatial image derivatives.
-
C++: void getDerivKernels(OutputArray kx, OutputArray ky, int dx, int dy, int ksize, bool normalize=false, int ktype=CV_32F )
-
Python: cv2.getDerivKernels(dx, dy, ksize[, kx[, ky[, normalize[, ktype]]]]) → kx, ky
| Parameters: |
- kx – Output matrix of row filter coefficients. It has the type ktype .
- ky – Output matrix of column filter coefficients. It has the type ktype .
- dx – Derivative order in respect of x.
- dy – Derivative order in respect of y.
- ksize – Aperture size. It can be CV_SCHARR , 1, 3, 5, or 7.
- normalize – Flag indicating whether to normalize (scale down) the filter coefficients or not. Theoretically, the coefficients should have the denominator
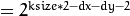 . If you are going to filter floating-point images, you are likely to use the normalized kernels. But if you compute derivatives of an 8-bit image, store the results in a 16-bit image, and wish to preserve all the fractional bits, you may want to set normalize=false . . If you are going to filter floating-point images, you are likely to use the normalized kernels. But if you compute derivatives of an 8-bit image, store the results in a 16-bit image, and wish to preserve all the fractional bits, you may want to set normalize=false .
- ktype – Type of filter coefficients. It can be CV_32f or CV_64F .
|
|---|
The function computes and returns the filter coefficients for spatial image derivatives. When ksize=CV_SCHARR , the Scharr
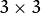 kernels are generated (see
Scharr() ). Otherwise, Sobel kernels are generated (see
Sobel() ). The filters are normally passed to
sepFilter2D() or to
kernels are generated (see
Scharr() ). Otherwise, Sobel kernels are generated (see
Sobel() ). The filters are normally passed to
sepFilter2D() or to
getGaussianKernel
Returns Gaussian filter coefficients.
-
C++: Mat getGaussianKernel(int ksize, double sigma, int ktype=CV_64F )
-
Python: cv2.getGaussianKernel(ksize, sigma[, ktype]) → retval
| Parameters: |
- ksize – Aperture size. It should be odd (
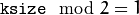 ) and positive. ) and positive.
- sigma – Gaussian standard deviation. If it is non-positive, it is computed from ksize as sigma = 0.3*((ksize-1)*0.5 - 1) + 0.8 .
- ktype – Type of filter coefficients. It can be CV_32F or CV_64F .
|
|---|
The function computes and returns the
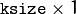 matrix of Gaussian filter coefficients:
matrix of Gaussian filter coefficients:
where
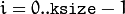 and
and
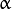 is the scale factor chosen so that
is the scale factor chosen so that
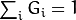 .
.
Two of such generated kernels can be passed to
sepFilter2D(). Those functions automatically recognize smoothing kernels (a symmetrical kernel with sum of weights equal to 1) and handle them accordingly. You may also use the higher-level
GaussianBlur().
getGaborKernel
Returns Gabor filter coefficients.
-
C++: Mat getGaborKernel(Size ksize, double sigma, double theta, double lambd, double gamma, double psi=CV_PI*0.5, int ktype=CV_64F )
-
Python: cv2.getGaborKernel(ksize, sigma, theta, lambd, gamma[, psi[, ktype]]) → retval
| Parameters: |
- ksize – Size of the filter returned.
- sigma – Standard deviation of the gaussian envelope.
- theta – Orientation of the normal to the parallel stripes of a Gabor function.
- lambd – Wavelength of the sinusoidal factor.
- gamma – Spatial aspect ratio.
- psi – Phase offset.
- ktype – Type of filter coefficients. It can be CV_32F or CV_64F .
|
|---|
For more details about gabor filter equations and parameters, see: Gabor Filter.
getStructuringElement
Returns a structuring element of the specified size and shape for morphological operations.
-
C++: Mat getStructuringElement(int shape, Size ksize, Point anchor=Point(-1,-1))
-
Python: cv2.getStructuringElement(shape, ksize[, anchor]) → retval
-
C: IplConvKernel* cvCreateStructuringElementEx(int cols, int rows, int anchor_x, int anchor_y, int shape, int* values=NULL )
-
The function constructs and returns the structuring element that can be further passed to
erode(),
dilate() or
morphologyEx() . But you can also construct an arbitrary binary mask yourself and use it as the structuring element.
Note
When using OpenCV 1.x C API, the created structuring element IplConvKernel* element must be released in the end using cvReleaseStructuringElement(&element).
morphologyEx
Performs advanced morphological transformations.
-
C++: void morphologyEx(InputArray src, OutputArray dst, int op, InputArray kernel, Point anchor=Point(-1,-1), int iterations=1, int borderType=BORDER_CONSTANT, const Scalar& borderValue=morphologyDefaultBorderValue() )
-
Python: cv2.morphologyEx(src, op, kernel[, dst[, anchor[, iterations[, borderType[, borderValue]]]]]) → dst
-
C: void cvMorphologyEx(const CvArr* src, CvArr* dst, CvArr* temp, IplConvKernel* element, int operation, int iterations=1 )
-
The function can perform advanced morphological transformations using an erosion and dilation as basic operations.
Opening operation:
Closing operation:
Morphological gradient:
“Top hat”:
“Black hat”:
Any of the operations can be done in-place. In case of multi-channel images, each channel is processed independently.
Note
- An example using the morphologyEx function for the morphological opening and closing operations can be found at opencv_source_code/samples/cpp/morphology2.cpp
Laplacian
Calculates the Laplacian of an image.
-
C++: void Laplacian(InputArray src, OutputArray dst, int ddepth, int ksize=1, double scale=1, double delta=0, int borderType=BORDER_DEFAULT )
-
Python: cv2.Laplacian(src, ddepth[, dst[, ksize[, scale[, delta[, borderType]]]]]) → dst
-
C: void cvLaplace(const CvArr* src, CvArr* dst, int aperture_size=3 )
| Parameters: |
- src – Source image.
- dst – Destination image of the same size and the same number of channels as src .
- ddepth – Desired depth of the destination image.
- ksize – Aperture size used to compute the second-derivative filters. See getDerivKernels() for details. The size must be positive and odd.
- scale – Optional scale factor for the computed Laplacian values. By default, no scaling is applied. See getDerivKernels() for details.
- delta – Optional delta value that is added to the results prior to storing them in dst .
- borderType – Pixel extrapolation method. See borderInterpolate for details.
|
|---|
The function calculates the Laplacian of the source image by adding up the second x and y derivatives calculated using the Sobel operator:
This is done when ksize > 1 . When ksize == 1 , the Laplacian is computed by filtering the image with the following
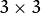 aperture:
aperture:
Note
- An example using the Laplace transformation for edge detection can be found at opencv_source_code/samples/cpp/laplace.cpp
pyrDown
Blurs an image and downsamples it.
-
C++: void pyrDown(InputArray src, OutputArray dst, const Size& dstsize=Size(), int borderType=BORDER_DEFAULT )
-
Python: cv2.pyrDown(src[, dst[, dstsize[, borderType]]]) → dst
-
C: void cvPyrDown(const CvArr* src, CvArr* dst, int filter=CV_GAUSSIAN_5x5 )
| Parameters: |
- src – input image.
- dst – output image; it has the specified size and the same type as src.
- dstsize – size of the output image.
- borderType – Pixel extrapolation method (BORDER_CONSTANT don’t supported). See borderInterpolate for details.
|
|---|
By default, size of the output image is computed as Size((src.cols+1)/2, (src.rows+1)/2), but in any case, the following conditions should be satisfied:
The function performs the downsampling step of the Gaussian pyramid construction. First, it convolves the source image with the kernel:
Then, it downsamples the image by rejecting even rows and columns.
pyrUp
Upsamples an image and then blurs it.
-
C++: void pyrUp(InputArray src, OutputArray dst, const Size& dstsize=Size(), int borderType=BORDER_DEFAULT )
-
Python: cv2.pyrUp(src[, dst[, dstsize[, borderType]]]) → dst
-
C: cvPyrUp(const CvArr* src, CvArr* dst, int filter=CV_GAUSSIAN_5x5 )
| Parameters: |
- src – input image.
- dst – output image. It has the specified size and the same type as src .
- dstsize – size of the output image.
- borderType – Pixel extrapolation method (only BORDER_DEFAULT supported). See borderInterpolate for details.
|
|---|
By default, size of the output image is computed as Size(src.cols*2, (src.rows*2), but in any case, the following conditions should be satisfied:
The function performs the upsampling step of the Gaussian pyramid construction, though it can actually be used to construct the Laplacian pyramid. First, it upsamples the source image by injecting even zero rows and columns and then convolves the result with the same kernel as in
pyrDown() multiplied by 4.
Note
- (Python) An example of Laplacian Pyramid construction and merging can be found at opencv_source_code/samples/python2/lappyr.py
pyrMeanShiftFiltering
Performs initial step of meanshift segmentation of an image.
-
C++: void pyrMeanShiftFiltering(InputArray src, OutputArray dst, double sp, double sr, int maxLevel=1, TermCriteria termcrit=TermCriteria(TermCriteria::MAX_ITER+TermCriteria::EPS,5,1) )
-
Python: cv2.pyrMeanShiftFiltering(src, sp, sr[, dst[, maxLevel[, termcrit]]]) → dst
-
C: void cvPyrMeanShiftFiltering(const CvArr* src, CvArr* dst, double sp, double sr, int max_level=1, CvTermCriteria termcrit=cvTermCriteria(CV_TERMCRIT_ITER+CV_TERMCRIT_EPS,5,1))
| Parameters: |
- src – The source 8-bit, 3-channel image.
- dst – The destination image of the same format and the same size as the source.
- sp – The spatial window radius.
- sr – The color window radius.
- maxLevel – Maximum level of the pyramid for the segmentation.
- termcrit – Termination criteria: when to stop meanshift iterations.
|
|---|
The function implements the filtering stage of meanshift segmentation, that is, the output of the function is the filtered “posterized” image with color gradients and fine-grain texture flattened. At every pixel
(X,Y) of the input image (or down-sized input image, see below) the function executes meanshift
iterations, that is, the pixel (X,Y) neighborhood in the joint space-color hyperspace is considered:
where (R,G,B) and (r,g,b) are the vectors of color components at (X,Y) and (x,y), respectively (though, the algorithm does not depend on the color space used, so any 3-component color space can be used instead). Over the neighborhood the average spatial value (X',Y') and average color vector (R',G',B') are found and they act as the neighborhood center on the next iteration:
After the iterations over, the color components of the initial pixel (that is, the pixel from where the iterations started) are set to the final value (average color at the last iteration):
When maxLevel > 0, the gaussian pyramid of maxLevel+1 levels is built, and the above procedure is run on the smallest layer first. After that, the results are propagated to the larger layer and the iterations are run again only on those pixels where the layer colors differ by more than sr from the lower-resolution layer of the pyramid. That makes boundaries of color regions sharper. Note that the results will be actually different from the ones obtained by running the meanshift procedure on the whole original image (i.e. when maxLevel==0).
Note
- An example using mean-shift image segmentation can be found at opencv_source_code/samples/cpp/meanshift_segmentation.cpp
sepFilter2D
Applies a separable linear filter to an image.
-
C++: void sepFilter2D(InputArray src, OutputArray dst, int ddepth, InputArray kernelX, InputArray kernelY, Point anchor=Point(-1,-1), double delta=0, int borderType=BORDER_DEFAULT )
-
Python: cv2.sepFilter2D(src, ddepth, kernelX, kernelY[, dst[, anchor[, delta[, borderType]]]]) → dst
-
The function applies a separable linear filter to the image. That is, first, every row of src is filtered with the 1D kernel kernelX . Then, every column of the result is filtered with the 1D kernel kernelY . The final result shifted by delta is stored in dst .
Smooth
Smooths the image in one of several ways.
-
C: void cvSmooth(const CvArr* src, CvArr* dst, int smoothtype=CV_GAUSSIAN, int size1=3, int size2=0, double sigma1=0, double sigma2=0 )
| Parameters: |
- src – The source image
- dst – The destination image
- smoothtype –
Type of the smoothing:
- CV_BLUR_NO_SCALE linear convolution with
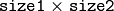 box kernel (all 1’s). If you want to smooth different pixels with different-size box kernels, you can use the integral image that is computed using integral() box kernel (all 1’s). If you want to smooth different pixels with different-size box kernels, you can use the integral image that is computed using integral()
- CV_BLUR linear convolution with
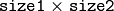 box kernel (all 1’s) with subsequent scaling by box kernel (all 1’s) with subsequent scaling by 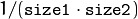
- CV_GAUSSIAN linear convolution with a
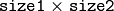 Gaussian kernel Gaussian kernel
- CV_MEDIAN median filter with a
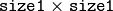 square aperture square aperture
- CV_BILATERAL bilateral filter with a
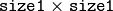 square aperture, color sigma= sigma1 and spatial sigma= sigma2 . If size1=0 , the aperture square side is set to cvRound(sigma2*1.5)*2+1 . Information about bilateral filtering can be found at http://www.dai.ed.ac.uk/CVonline/LOCAL_COPIES/MANDUCHI1/Bilateral_Filtering.html square aperture, color sigma= sigma1 and spatial sigma= sigma2 . If size1=0 , the aperture square side is set to cvRound(sigma2*1.5)*2+1 . Information about bilateral filtering can be found at http://www.dai.ed.ac.uk/CVonline/LOCAL_COPIES/MANDUCHI1/Bilateral_Filtering.html
- size1 – The first parameter of the smoothing operation, the aperture width. Must be a positive odd number (1, 3, 5, ...)
- size2 – The second parameter of the smoothing operation, the aperture height. Ignored by CV_MEDIAN and CV_BILATERAL methods. In the case of simple scaled/non-scaled and Gaussian blur if size2 is zero, it is set to size1 . Otherwise it must be a positive odd number.
- sigma1 –
In the case of a Gaussian parameter this parameter may specify Gaussian 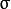 (standard deviation). If it is zero, it is calculated from the kernel size: (standard deviation). If it is zero, it is calculated from the kernel size:
Using standard sigma for small kernels ( 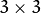 to to 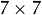 ) gives better speed. If sigma1 is not zero, while size1 and size2 are zeros, the kernel size is calculated from the sigma (to provide accurate enough operation). ) gives better speed. If sigma1 is not zero, while size1 and size2 are zeros, the kernel size is calculated from the sigma (to provide accurate enough operation).
|
|---|
The function smooths an image using one of several methods. Every of the methods has some features and restrictions listed below:
- Blur with no scaling works with single-channel images only and supports accumulation of 8-bit to 16-bit format (similar to Sobel() and Laplacian()) and 32-bit floating point to 32-bit floating-point format.
- Simple blur and Gaussian blur support 1- or 3-channel, 8-bit and 32-bit floating point images. These two methods can process images in-place.
- Median and bilateral filters work with 1- or 3-channel 8-bit images and can not process images in-place.
Sobel
Calculates the first, second, third, or mixed image derivatives using an extended Sobel operator.
-
C++: void Sobel(InputArray src, OutputArray dst, int ddepth, int dx, int dy, int ksize=3, double scale=1, double delta=0, int borderType=BORDER_DEFAULT )
-
Python: cv2.Sobel(src, ddepth, dx, dy[, dst[, ksize[, scale[, delta[, borderType]]]]]) → dst
-
C: void cvSobel(const CvArr* src, CvArr* dst, int xorder, int yorder, int aperture_size=3 )
-
In all cases except one, the
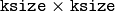 separable kernel is used to calculate the
derivative. When
separable kernel is used to calculate the
derivative. When
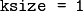 , the
, the
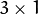 or
or
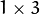 kernel is used (that is, no Gaussian smoothing is done). ksize = 1 can only be used for the first or the second x- or y- derivatives.
kernel is used (that is, no Gaussian smoothing is done). ksize = 1 can only be used for the first or the second x- or y- derivatives.
There is also the special value ksize = CV_SCHARR (-1) that corresponds to the
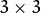 Scharr
filter that may give more accurate results than the
Scharr
filter that may give more accurate results than the
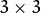 Sobel. The Scharr aperture is
Sobel. The Scharr aperture is
for the x-derivative, or transposed for the y-derivative.
The function calculates an image derivative by convolving the image with the appropriate kernel:
The Sobel operators combine Gaussian smoothing and differentiation,
so the result is more or less resistant to the noise. Most often,
the function is called with ( xorder = 1, yorder = 0, ksize = 3) or ( xorder = 0, yorder = 1, ksize = 3) to calculate the first x- or y- image
derivative. The first case corresponds to a kernel of:
The second case corresponds to a kernel of:
Scharr
Calculates the first x- or y- image derivative using Scharr operator.
-
C++: void Scharr(InputArray src, OutputArray dst, int ddepth, int dx, int dy, double scale=1, double delta=0, int borderType=BORDER_DEFAULT )
-
Python: cv2.Scharr(src, ddepth, dx, dy[, dst[, scale[, delta[, borderType]]]]) → dst
| Parameters: |
- src – input image.
- dst – output image of the same size and the same number of channels as src.
- ddepth – output image depth (see Sobel() for the list of supported combination of src.depth() and ddepth).
- dx – order of the derivative x.
- dy – order of the derivative y.
- scale – optional scale factor for the computed derivative values; by default, no scaling is applied (see getDerivKernels() for details).
- delta – optional delta value that is added to the results prior to storing them in dst.
- borderType – pixel extrapolation method (see borderInterpolate for details).
|
|---|
The function computes the first x- or y- spatial image derivative using the Scharr operator. The call
is equivalent to
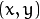 in the source image (normally, rectangular), its neighborhood is considered and used to compute the response. In case of a linear filter, it is a weighted sum of pixel values. In case of morphological operations, it is the minimum or maximum values, and so on. The computed response is stored in the destination image at the same location
in the source image (normally, rectangular), its neighborhood is considered and used to compute the response. In case of a linear filter, it is a weighted sum of pixel values. In case of morphological operations, it is the minimum or maximum values, and so on. The computed response is stored in the destination image at the same location
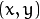 . It means that the output image will be of the same size as the input image. Normally, the functions support multi-channel arrays, in which case every channel is processed independently. Therefore, the output image will also have the same number of channels as the input one.
. It means that the output image will be of the same size as the input image. Normally, the functions support multi-channel arrays, in which case every channel is processed independently. Therefore, the output image will also have the same number of channels as the input one.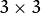 filter, then, when processing the left-most pixels in each row, you need pixels to the left of them, that is, outside of the image. You can let these pixels be the same as the left-most image pixels (“replicated border” extrapolation method), or assume that all the non-existing pixels are zeros (“constant border” extrapolation method), and so on.
OpenCV enables you to specify the extrapolation method. For details, see the function borderInterpolate and discussion of the borderType parameter in the section and various functions below.
filter, then, when processing the left-most pixels in each row, you need pixels to the left of them, that is, outside of the image. You can let these pixels be the same as the left-most image pixels (“replicated border” extrapolation method), or assume that all the non-existing pixels are zeros (“constant border” extrapolation method), and so on.
OpenCV enables you to specify the extrapolation method. For details, see the function borderInterpolate and discussion of the borderType parameter in the section and various functions below.
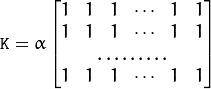
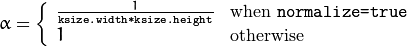
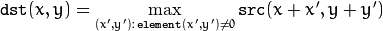
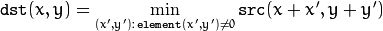
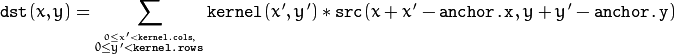
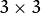 kernels are generated (see
Scharr() ). Otherwise, Sobel kernels are generated (see
Sobel() ). The filters are normally passed to
sepFilter2D() or to
kernels are generated (see
Scharr() ). Otherwise, Sobel kernels are generated (see
Sobel() ). The filters are normally passed to
sepFilter2D() or to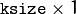 matrix of Gaussian filter coefficients:
matrix of Gaussian filter coefficients: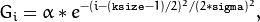
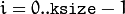 and
and
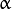 is the scale factor chosen so that
is the scale factor chosen so that
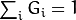 .
. aperture. Each channel of a multi-channel image is processed independently. In-place operation is supported.
aperture. Each channel of a multi-channel image is processed independently. In-place operation is supported.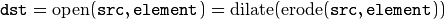
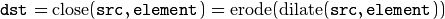
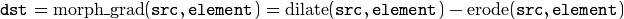
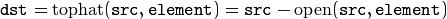
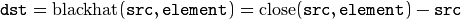
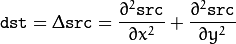
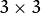 aperture:
aperture: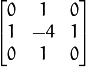
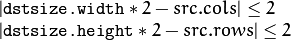
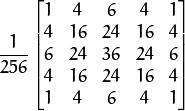
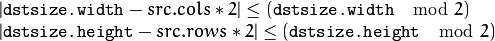
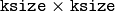 separable kernel is used to calculate the
derivative. When
separable kernel is used to calculate the
derivative. When
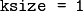 , the
, the
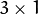 or
or
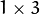 kernel is used (that is, no Gaussian smoothing is done). ksize = 1 can only be used for the first or the second x- or y- derivatives.
kernel is used (that is, no Gaussian smoothing is done). ksize = 1 can only be used for the first or the second x- or y- derivatives.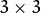 Scharr
filter that may give more accurate results than the
Scharr
filter that may give more accurate results than the
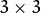 Sobel. The Scharr aperture is
Sobel. The Scharr aperture is